 Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas.
Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas.
Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
Binomio al cuadrado o cuadrado de un binomio
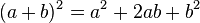
Ejemplo:

Producto de dos binomios con un término común
Ejemplo:

Producto de dos binomios conjugados
- Ejemplo:

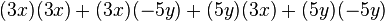
Polinomio al cuadrado

- Ejemplo:
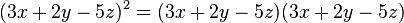

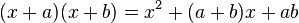
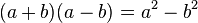
Comentarios
Publicar un comentario